Fundamentals of Fracture Mechanics
In our course so far, we have focused on how bodies deform under load. Now, we will ask a different question: when do they break?
The field that studies how cracks initiate and grow in materials is called fracture mechanics. To understand it, we’ll start with a simple, fundamental principle: breaking things costs energy. To explain this, we will use an analogy of a spring with a weak link. Imagine a block attached to a wall by a spring. When we pull on the block, the spring stretches and stores elastic potential energy, \(\Psi_{elastic}\).
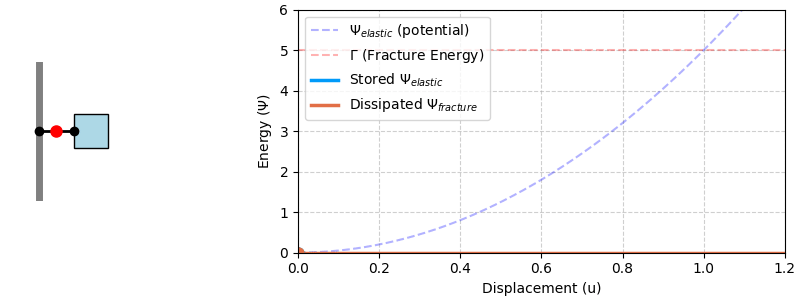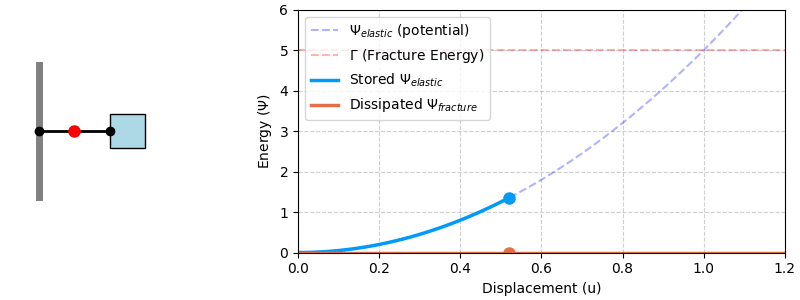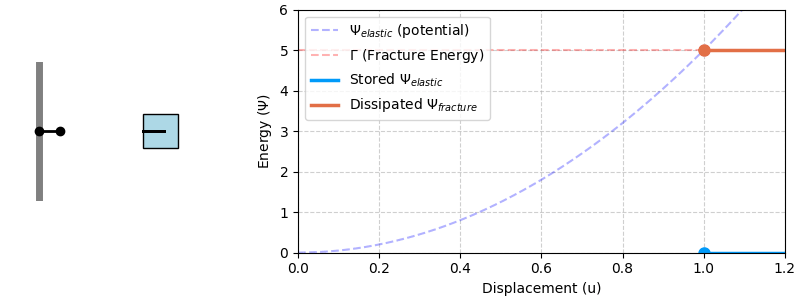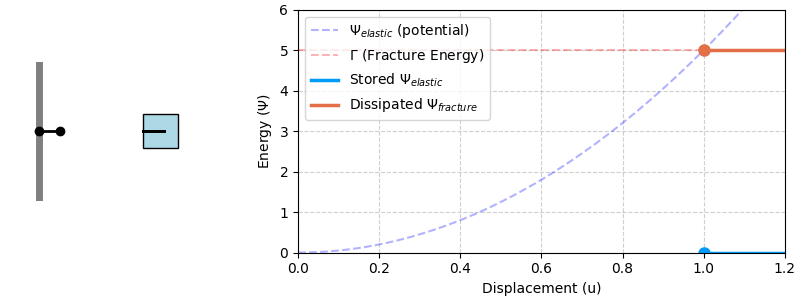
Now, imagine the spring has a single “weak link” that will snap if enough energy is provided. The moment the link snaps, the stretched spring unloads. The elastic energy stored in the system suddenly decreases. This is the energy that becomes available to drive the “fracture.” The process of snapping the link itself requires a certain amount of energy to break the material bonds. This is the “fracture energy” or toughness of the link. The link will only break if the elastic energy released by the system is greater than or equal to the energy required to break the link. This simple energy balance is the key to understanding all of fracture mechanics.
Fracture Mechanics: Energy perspective
The energy criterion, pioneered by Griffith (1920) and extended by Irwin (1956), defines fracture based on energy balance. Fracture mechanics, viewed from an energy perspective, centers on the concept that crack extension occurs when the energy available to drive the crack is sufficient to overcome the material’s resistance to fracture. This framework began with Griffith and was extended by Orowan and Irwin to form the basis of modern fracture mechanics. The core idea is that a crack will only grow if the energy released by the system is sufficient to overcome the energy required to create the new crack surfaces.
Imagine a stretched rubber band. It stores elastic strain energy. When it snaps, that stored energy is violently released as kinetic energy, sound, and heat. Griffith’s theory is the formalization of this concept for a crack.
- Energy Source: As a crack grows, the material around it unloads, releasing stored elastic strain energy. This is the energy that “powers” the fracture.
- Energy Sink: Creating a new surface requires breaking atomic bonds, which consumes energy. This is a material property called the surface energy or fracture energy.
Therefore, the fundamental concepts in fracture mechanics are fracture energy (material resistance) and energy release rate (driving force).
Fracture energy density (\(\Gamma\))
Fracture energy density (\(\Gamma\)) represents the total energy dissipated per unit area of newly created crack surfaces. This energy constitutes the material’s resistance to crack extension. For an ideally brittle solids (like glass, as studied by Griffith), the resistance to fracture is solely the energy required to create the new crack surfaces known as surface energy \(\gamma_s\). This is the energy required to create a new surface of unit area i.e \(\text{J/m}^2\). Since fracture results in the creation of two new surfaces, the total fracture energy is given by:
\[\Gamma = 2 \gamma_s\]
Let us assume if the total amount of energy dissipated by the system is \(\Delta \Psi_\text{fracture}\) when the crack is extended by an amount \(\Delta a\). Then, the fracture energy density is given by: \[ \Gamma = \frac{\Delta \Psi_\text{fracture}}{\Delta a} = \frac{\text{d} \Psi_\text{fracture}}{\text{d}a} \]
Fracture energy is a material property and hence, it is a local property. This is often referred to as the fracture toughness of the material.
Energy Release Rate (\(G\))
The energy release rate (G), often called the energy flux in a more general context, is defined as the rate of change in potential energy (\(\Psi\)) with respect to crack length (\(a\)):
\[G = -\frac{\text{d}\Psi}{\text{d}a}\]
\(G\) is interpreted as the crack driving force, the amount of energy supplied by the elastic energy in the body and by the loading system in creating the new fracture surface per unit crack advance
Energy release rate depends on the global geometry, the applied loads, and the material properties. Hence, it is a global property.
Relation between Driving Force \(G\) and Fracture Energy \(\Gamma\)
Imagine a elastic body with a crack of length \(a\). The body is loaded by a force \(F\) and the crack is extended by an amount \(\text{d}a\). The total potential energy of the system, externally loaded, when the crack is extended by an amount \(\text{d}a\) is given by: \[ \Psi = \Psi_\text{elastic} - \Psi_\text{ext} + \Psi_\text{fracture} \] where \(\Psi_\text{elastic}\) is the elastic strain energy, \(\Psi_\text{ext}\) is the external work done on the system, and \(\Psi_\text{fracture}\) is the energy that is created due to the crack extension.
The rate of change of potential energy with respect to crack length is given by: \[ \frac{\text{d}\Psi}{\text{d}a} = \frac{\text{d}\Psi_\text{elastic}}{\text{d}a} - \frac{\text{d}\Psi_\text{ext}}{\text{d}a} + \frac{\text{d}\Psi_\text{fracture}}{\text{d}a} \]
For a system in equilibrium, the rate of change of potential energy with respect to crack extension is zero i.e a minimum potential energy. Therefore, we have: \[ \underbrace{-\big(\frac{\text{d}\Psi_\text{elastic}}{\text{d}a} - \frac{\text{d}\Psi_\text{ext}}{\text{d}a}\big)}_{G} = \underbrace{\frac{\text{d}\Psi_\text{fracture}}{\text{d}a}}_{\Gamma} \]
Therefore, the crack extension will occur if the energy release rate is equal to the fracture energy density. \[G = \Gamma\]
The above equation states that the energy flow (flux) to the crack edge region must be sufficient to support the processes leading to material separation at the crack tip.
This relation is equating a global property (energy release rate) with a local property (fracture energy density).
Calculation of Energy Release Rate \(G\)
While we can compute \(G\) numerically by simulating two slightly different crack lengths (as you will do in the exercise), LEFM provides a powerful analytical shortcut. For many standard geometries, the energy release rate \(G\) has been pre-calculated. For a plate of width \(W\) with a central crack of length \(2a\) under a remote stress \(\sigma_\infty\), the formula is: \[G = (\sigma_\infty \sqrt{\pi a} F(a/W))^2 \frac{1}{E'}\]
where \(E'\) is the effective elastic modulus, \(E'\) = \(E\) for plane stress and \(E'\) = \(E / (1-\nu^2)\) for plane strain. \(F(a/W)\) is a dimensionless function of the crack length \(a\) and the plate width \(W\). \(\sigma_\infty\) is the remote tensile stress.
Historically, this formula is often derived via an intermediate parameter called the Stress Intensity Factor \(K_I\). You will see the relation \(G = K_I^2 / E'\) throughout the literature. While we are focusing on energy, it’s important to recognize that \(K_I\) is simply the parameter that encapsulates the geometry and loading effects (\(K_I = \sigma_\infty \sqrt{\pi a} F(a/W)\)).
Griffith’s Critical Crack Length
From the above two relations i.e
\[ G = \Gamma = \frac{K_I^2}{E'} \]
we can estimate the critical crack length \(a_c\) in a plate which when subjected to a remote tensile stress \(\sigma_\infty\). Equating the two relations, we get
\[ a_c = \dfrac{1}{\pi}\frac{\Gamma E } {(1-\nu^2 )\sigma_\infty^2} \]
All the above fundamental concepts consitutes the Linear Elastic Fracture Mechanics (LEFM) framework.
The derivation of \(G=\frac{K_I^2}{E'}\) is rigorously confined by the assumptions of LEFM
Linear Elasticity: The material must be isotropic and obey Hooke’s law
Quasistatic Conditions: The deformation must be quasistatic, meaning inertial and rate effects are negligible
Infinitesimally Small Scale Yielding (SSY): The derivation depends on being able to shrink the dissipative region to the crack edge (“point model”). This means any inelastic deformation must be confined to a region that is negligibly small compared to the crack length and other dimensions
If the conditions allow for small scale yielding but not strictly infinitesimal yielding, the relationship \(G=\frac{K_I^2}{E'}\) still characterizes the energy flow. However, the framework of LEFM loses validity when the fracture process zone size becomes large relative to key dimension.
The Limits of LEFM: The Fracture Process Zone (FPZ)
The framework we’ve just described is called Linear Elastic Fracture Mechanics (LEFM). It’s incredibly powerful, but it’s built on a contradiction: the stress singularity predicts infinite stress, which is physically impossible, because this will means any infinitismall stress will break the material, which is not the case. Real materials have finite strength. In reality, the material in a very small region directly ahead of the crack tip does not behave elastically. It yields, forms micro-voids, breaks fibers, and undergoes other irreversible, nonlinear deformation processes. This tiny, “messy” region of inelastic behavior is called the Fracture Process Zone (FPZ) or the Inelastic Zone.
LEFM is an asymptotic theory. It is only accurate outside the FPZ, but still close to the crack tip.
- Very far from the tip: The stress field is complex and depends on the global geometry.
- Close to the tip (but outside the FPZ): The stress field beautifully matches the \(\frac{1}{\sqrt{r}}\) solution. This is the region of K-dominance.
- Inside the FPZ: LEFM is invalid. The stresses are high but finite, and the material is failing.
The Computational Bridge: Cohesive Zone Models (CZM)
Since LEFM breaks down inside the FPZ, how can we numerically simulate the entire process of crack initiation and propagation?
This is where Cohesive Zone Models (CZM) come in. A CZM replaces the unphysical stress singularity of LEFM with a traction-separation law that describes the physics happening inside the FPZ.
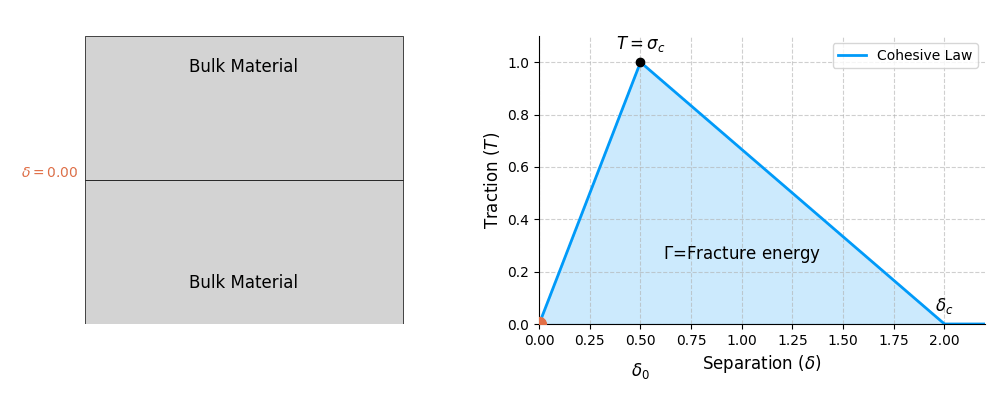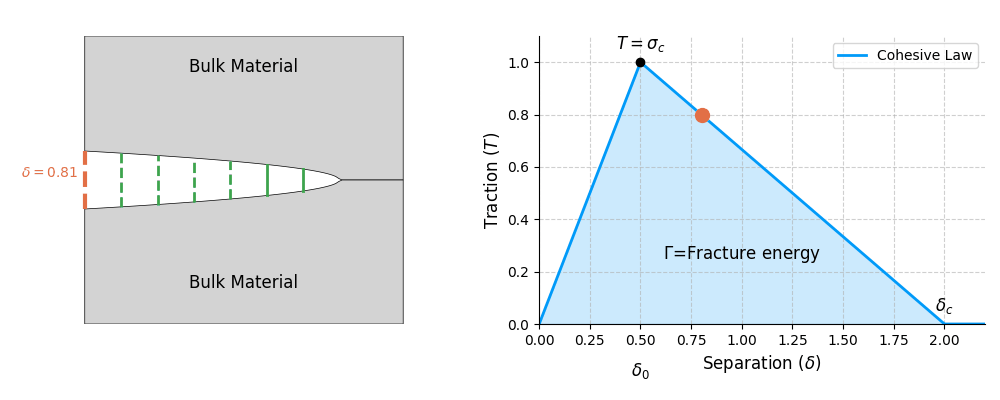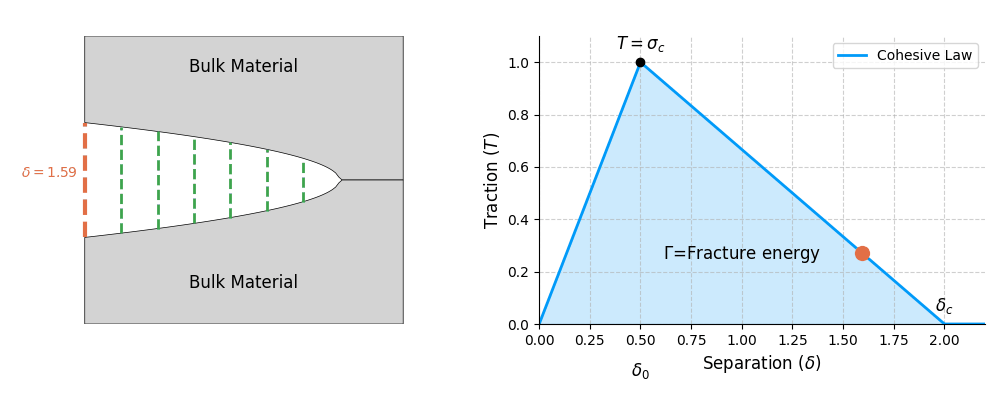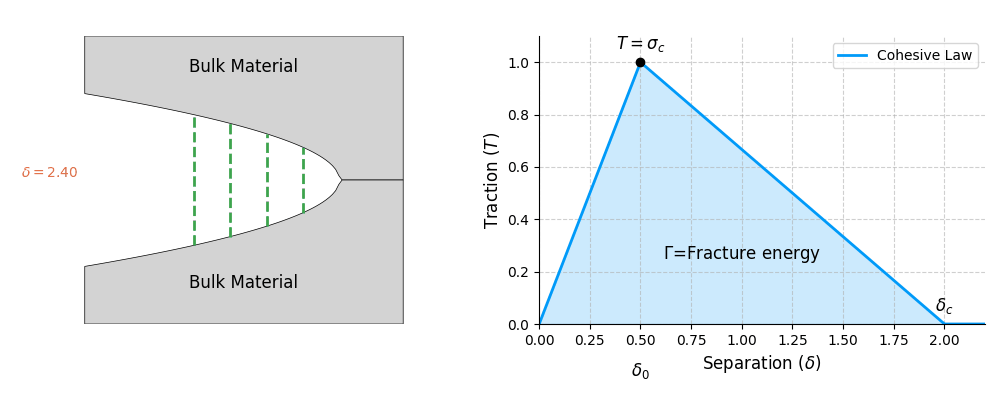
Cohesive zone modelling is a numerical technique to model the fracture of materials. It is based on the idea that as a material fracture (or breaks), the micro-cracks (or damage) is restricted in a small region in front of the crack-tip (see Figure). This region is termed the cohesive zone, which is a region where the material is in state of breakage. The size of cohesive zone depends on the material. For example, in a brittle material, the cohesive zone is very small, while in a ductile material, the cohesive zone is larger.
One can think of the size of cohesive zone is small, it resembles the small-scale yielding zone as assumed in Linear Elastic Fracture Mechanics. What this means that all the inelastic or nonlinear process related to fracture are confined to the cohesive zone and the rest of the material is assumed to be linear elastic. And in theory, the stress field outside of the cohesive zone is the same as the stress field as predicted by Linear Elastic Fracture Mechanics.
In reality, the separation process inside the cohesive zone is quite complex. Inside the cohesive zone, the material is in state of breakage _i.e._uneven breakage of material fibres, formation of micro-cracks and micro-voids, coalescence of micro-voids and formation of a macro-crack. Hence, the separation process is not uniform along the cohesive zone and is gradual. This process and its characteristics are dependent on the material. For example, in a brittle material, the separation process is sudden and sharp, while in a ductile material, the separation process is gradual and smooth. As a result, the entire separation process is often approximated by a simple function which is called the traction-separation law. These traction-separation laws describes the behaviour of the material inside the cohesive zone.
Traction-separation laws
The response of the cohesive zone is characterized by a traction-separation law, which relates the traction \(T\) to the separation \(\delta\) of the two surfaces of the cohesive zone. The functional form of the traction-separation law represents how the material within the cohesive zone behaves as it is being pulled apart. Ideally, the traction-separation law would be highly nonlinear, with a initial ascending branch, a peak, and a descending branch. The ascending branch is the initial elastic behaviour of the material, the peak is the maximum strength of the material (the critical strength at which the material starts to break), and the descending branch is the post-peak behaviour of the material. The post-peak behvaior captures all the inelastic or nonlinear processes related to material fibre breakage, formation of micro-cracks and micro-voids, coalescence of micro-voids and formation of a macro-crack.
A traction-separation law is characterized by two material parameters:
- critical strength, \(\sigma_c\)
- fracture energy, \(\Gamma\)
Another parameter is the critical separation \(\delta_c\) which is the separation of the two surfaces of the cohesive zone at which the material starts to break. However, in practice, the critical separation is not always easy to measure. Therefore, we often use the fracture energy \(\Gamma\) and the critical strength \(\sigma_c\) to characterize the material. The fracture energy \(\Gamma\) is the area under the traction-separation curve until the critical separation \(\delta_c\) is reached. This is the energy required to create a new surface of unit area i.e \(\text{J/m}^2\). Therefore, the fracture energy is given by:
\[ \Gamma = \psi(\delta_c) ~ \text{ where } ~\psi(\delta) = \int_0^{\delta} T(\delta) \text{d}\delta\]
\(\delta\) is the separation of the two surfaces within the cohesive zone that will eventually be separated, \(\psi(\delta)\) is the work done per unit area of cohesive zone in separating the two surfaces of the cohesive zone by an amount \(\delta\) and \(\Gamma\) is the fracture energy of the material.
Physically this means that the amount of work done (per unit area of cohesive zone) in completely separating the two surfaces of the cohesive zone is equal to the fracture energy of the material
Analogy to Penalty Method or Spring Model
To understand what exactly a traction-separation law is, let us consider the following analogy: Imagine a line of tiny, breakable springs laid out along the potential crack path.
- As the material is pulled apart, these springs stretch and resist, representing the cohesive tractions (\(T(\delta)\)) holding the material together. The spring is in state of elastic deformation until the critical strength \(\sigma_c\) is reached.
- As they stretch further (reach a critical strength \(\sigma_c\)), they begin to “soften” and lose strength, representing material damage.
- Finally, when they reach a critical separation \(\delta_c\), they break completely, and a true, stress-free crack surface is formed.
If one had to write the work done per unit area in extending the spring by an amount \(\delta\), it would be given by:
\[ \psi(\delta) = \int_0^{\delta} \underbrace{\kappa \delta}_{T(\delta)} \text{d}\delta \]
where \(\kappa\) is the spring constant or spring stiffness and \(\delta\) is the extension of the spring.
Thus, the traction-separation law inside the cohesive zone can be understood as the work done per unit area in extending the spring which is holding the two surfaces of the cohesive zone together. Instead of a constant spring stiffness, the spring stiffness is a function of the separation \(\delta\). As the separation increases, the spring stiffness decreases and finally reaches zero at the critical separation \(\delta_c\). If you notice, the cohesive zone model is nothing more than a penalty method to enforce the two surfaces of the solids to stick together for a sometime and then break apart. In (sec?)-
Energy functional for fracture
USing the cohesive zone model, we can write the energy functional for a solid body undergoing fracture as:
\[ \Psi = \Psi_\text{elastic} - \Psi_\text{external} + \Psi_\text{fracture} \]
where \(\Psi_\text{elastic}\) is the elastic energy, \(\Psi_\text{external}\) is the work done by the external forces, and \(\Psi_\text{fracture}\) is the fracture energy that is dissipated in creating new fracturesurfaces.
The fracture energy is the total energy dissipated in creating new fracture surfaces. From cohesive zone modelling, we know that the work done per unit area in separating the two surfaces of the cohesive zone by an amount \(\delta\) is given by \(\psi(\delta)\). Therefore, the total fracture energy is given by:
\[ \Psi_\text{fracture} = \int_{\Gamma_{coh}} \psi(\delta) \text{d}a \]
where \(\Gamma_\text{coh}\) is the crack path.
As we know from fracture mechanics theory that if a crack propagates by \(\text{d}a\), the rate of change of fracture energy \(\Psi_\text{fracture}\) with respect to the crack length \(a\) gives the fracture toughness \(\Gamma\). Therefore, we can write:
\[ \Gamma = \frac{\text{d}\Psi_\text{fracture}}{\text{d}a} \] Since we said earlier that a TSL is chosen such that the \(\psi(\delta) = \Gamma\) at \(\delta = \delta_c\). Therefore, we always maintain the above relation which will only allow the crack to propagate if the energy is dissipated in creating new fracture surfaces is equal to the fracture toughness. Thus maintaining the fracture criterion.
As we have seen above, the TSL and its functional form is crucial as it determines the total fracture energy. We can either define a TSL using the relationship between the traction and the separation (\(T(\delta)\)) or the relationship between the work done per unit area and the separation (\(\psi(\delta)\)).
Common Traction-Separation Laws
While the true Traction-Separation Law (TSL) is complex, we use simple mathematical forms for numerical simulations. The choice of shape defines the relationship between the key parameters. For this course, we will use the bilinear law and the exponential law.
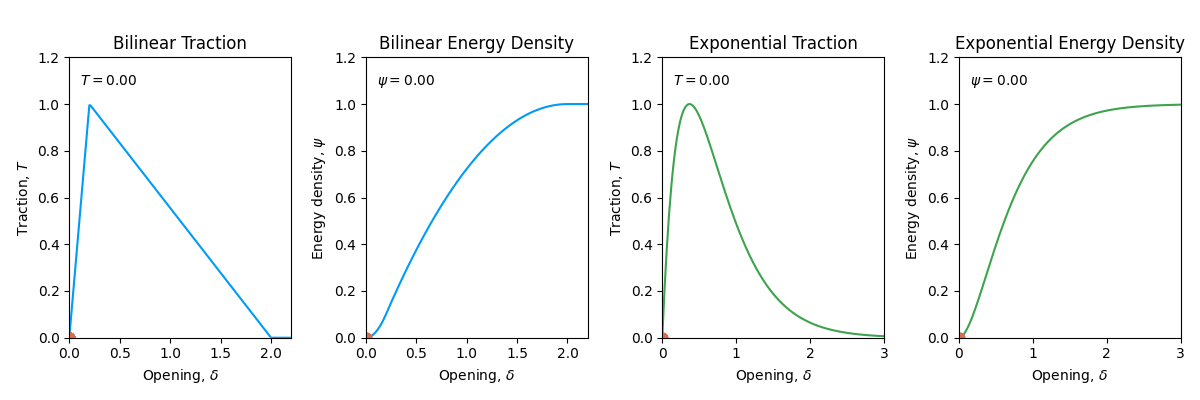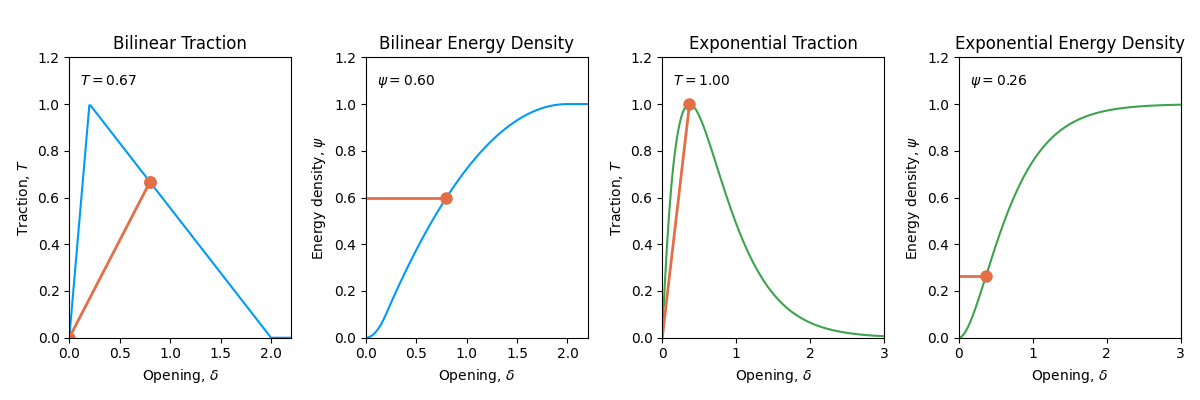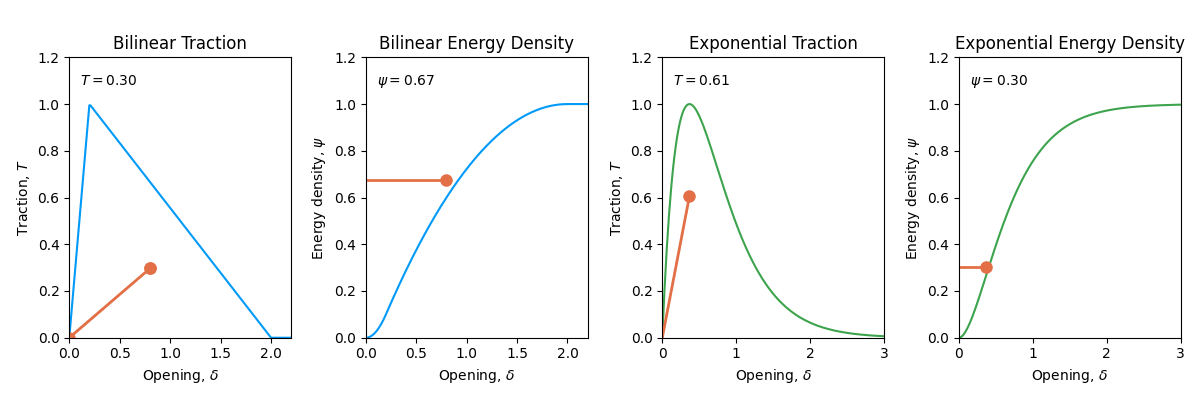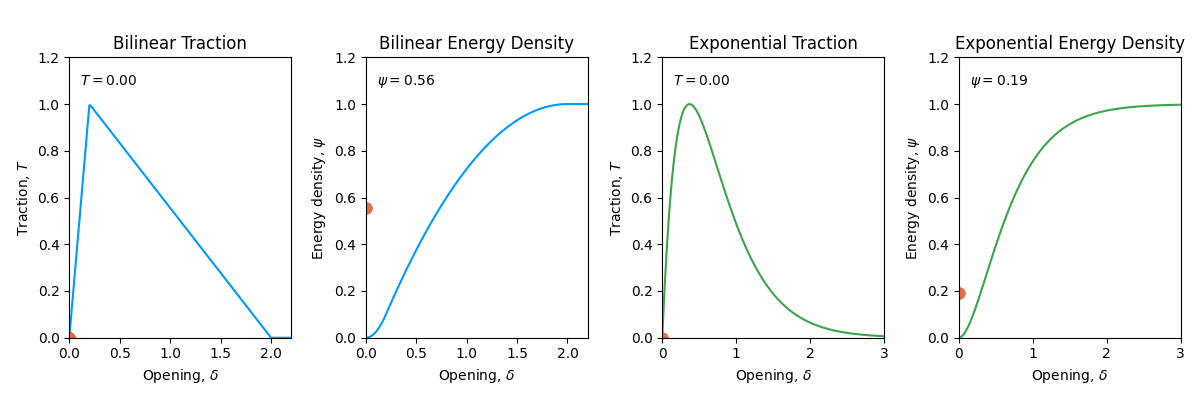
Bilinear Law: This is a simple Traction-Separation Law that is often used to model brittle fracture. It has an initial elastic stiffness \(K\) before damage begins, which is more physically realistic. The TSL thus takes the form:
\[T(\delta) = \begin{cases} \sigma_c \dfrac{\delta}{\delta_c} & \text{if } \delta \leq \delta_c \\ \sigma_c (1 - (\delta - \delta_c) / (\delta_f - \delta_c)) & \text{if } \delta > \delta_c \text{ and } \delta \leq \delta_f \\ 0 & \text{if } \delta > \delta_f \end{cases}\]
where \(\sigma_c\) is the critical strength and \(\delta_c\) is the critical separation and \(\delta_f\) is the separation at which the material completely separates given by \(\delta_f = 2\Gamma / \sigma_c\) . Figure 14.2 shows the TSL for the bilinear law.
In terms of the work done per unit area, the bilinear law is given by:
\[ \psi(\delta) = \begin{cases} \frac{1}{2} \dfrac{\sigma_c}{\delta_c} \delta^2 & \text{if } \delta \leq \delta_c \\ \dfrac{1}{2}\sigma_c \delta_f - \dfrac{1}{2}\sigma_c(\delta_f - \delta)^2 / (\delta_f - \delta_c)) & \text{if } \delta > \delta_c \text{ and } \delta \leq \delta_f \\ \dfrac{1}{2}\sigma_c \delta_f & \text{if } \delta > \delta_f \end{cases} \]
Exponential Law: This law provides a smooth softening curve, which can be more stable in some numerical simulations. The TSL relationship is given by
\[ T(\delta) = \frac{\Gamma}{\delta_c^2} \cdot \delta \cdot e^{- \delta / \delta_c} ~\text{where}~ \delta_c = \frac{\Gamma e^{-1}}{\sigma_c} \]
If you notice that the exponential law (see Figure 14.2) is the same as the bilinear law when \(\delta_f = \infty\). This means that there will always be some residual strength in the material even after the material has completely separated.
Similarily, in terms of the work done per unit area, the exponential law is given by:
\[ \psi(\delta) = \Gamma \cdot (1 - (1+\delta / \delta_c) \cdot e^{- \delta / \delta_c}) \]
Irreversibility in the Traction-Separation Law
A fracture process is irreversible. This means that once the material has started to break or has dissipated some energy, it will cannot recover that energy and thus cannot heal. Therefore, the traction-separation law should be such that the material can only break once. This is known as the irreversibility of the traction-separation law. In Figure 14.2, we show how concept of irreversibility is introduced in the cohesive zone model. When the material is unloading, \(\delta\) is decreasing, the traction-separation law and the potential energy \(\psi(\delta)\) no longer follow the original curve. The energy density \(\psi(\delta)\) decreases because the material is partially damaged and therefore it can recover some of the energy.
To introduce irreversibility in the traction-separation law, we keep track of the opening \(\delta\) and associate a \(\delta_\text{max}\) value with it. This \(\delta_\text{max}\) value is the maximum separation of the two surfaces of the cohesive zone. If at any point during the simulation, the opening \(\delta < \delta_\text{max}\), then it means that the cohesive zone is unloading and we need to introduce the irreversibility in the traction-separation law.
\[ \psi(\delta) = \begin{cases} \psi(\delta) & \text{if } \delta = \delta_\text{max} \\ \psi(\delta_\text{max}) - \dfrac{1}{2}(\delta_\text{max} - \delta) \times (T(\delta_\text{max}) + \frac{T(\delta_\text{max}) \delta}{\delta_\text{max}}) & \text{if } \delta < \delta_\text{max} \end{cases} \]